this post was submitted on 23 Feb 2025
497 points (99.2% liked)
Lemmy Shitpost
28457 readers
3226 users here now
Welcome to Lemmy Shitpost. Here you can shitpost to your hearts content.
Anything and everything goes. Memes, Jokes, Vents and Banter. Though we still have to comply with lemmy.world instance rules. So behave!
Rules:
1. Be Respectful
Refrain from using harmful language pertaining to a protected characteristic: e.g. race, gender, sexuality, disability or religion.
Refrain from being argumentative when responding or commenting to posts/replies. Personal attacks are not welcome here.
...
2. No Illegal Content
Content that violates the law. Any post/comment found to be in breach of common law will be removed and given to the authorities if required.
That means:
-No promoting violence/threats against any individuals
-No CSA content or Revenge Porn
-No sharing private/personal information (Doxxing)
...
3. No Spam
Posting the same post, no matter the intent is against the rules.
-If you have posted content, please refrain from re-posting said content within this community.
-Do not spam posts with intent to harass, annoy, bully, advertise, scam or harm this community.
-No posting Scams/Advertisements/Phishing Links/IP Grabbers
-No Bots, Bots will be banned from the community.
...
4. No Porn/Explicit
Content
-Do not post explicit content. Lemmy.World is not the instance for NSFW content.
-Do not post Gore or Shock Content.
...
5. No Enciting Harassment,
Brigading, Doxxing or Witch Hunts
-Do not Brigade other Communities
-No calls to action against other communities/users within Lemmy or outside of Lemmy.
-No Witch Hunts against users/communities.
-No content that harasses members within or outside of the community.
...
6. NSFW should be behind NSFW tags.
-Content that is NSFW should be behind NSFW tags.
-Content that might be distressing should be kept behind NSFW tags.
...
If you see content that is a breach of the rules, please flag and report the comment and a moderator will take action where they can.
Also check out:
Partnered Communities:
1.Memes
10.LinuxMemes (Linux themed memes)
Reach out to
All communities included on the sidebar are to be made in compliance with the instance rules. Striker
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
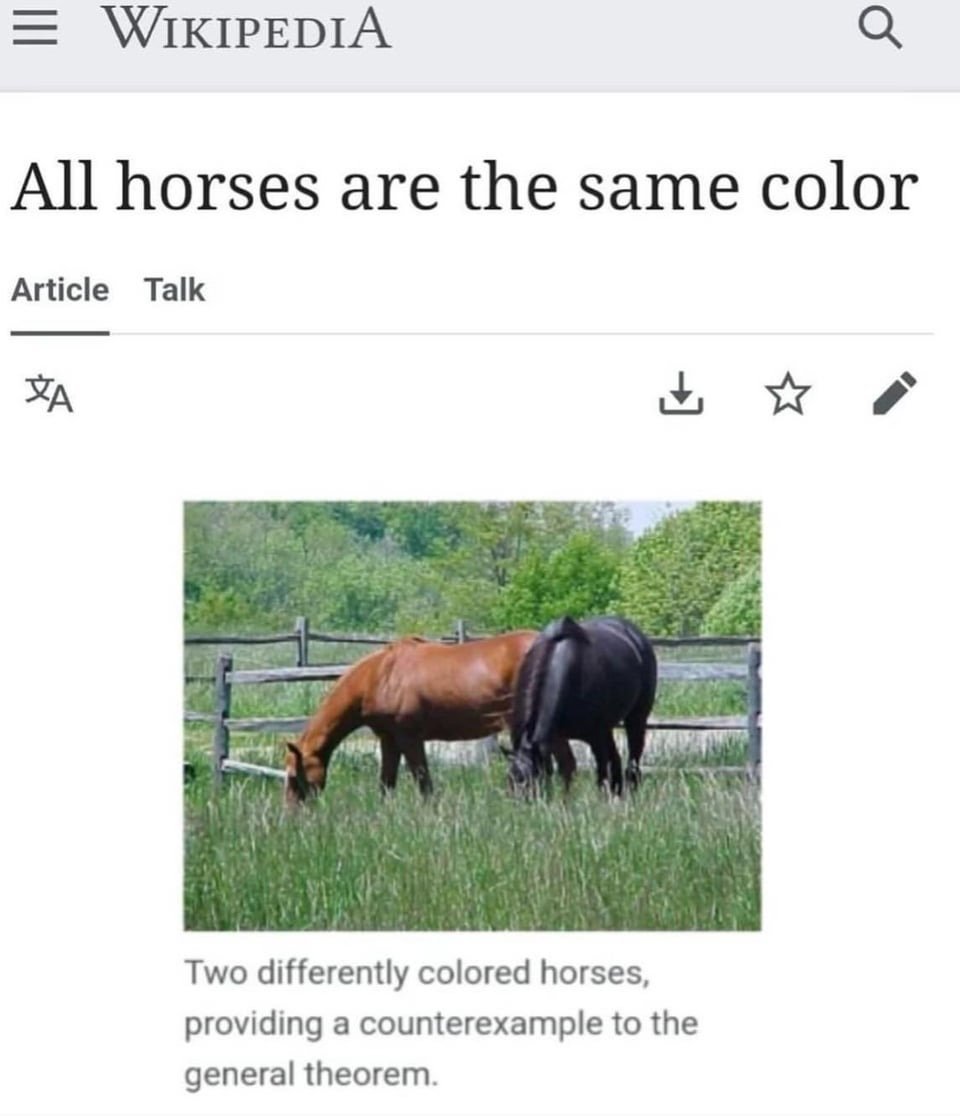
I did do this proof by induction back in the day, but now looking at the article I am clueless.
Do you mean you went through the proof and verified it, or falsified it?
As I understand it, it goes something like this:
...
You have a set of n horses.
Assume a set of n horses are the same color.
Now you also have a set of n+1 horses.
Set 1: (1, 2, 3, ... n)
Set 2: (2, 3, 4, ... n+1)
Referring back to the assumption, both sets have n horses in them, Set 2 is just incremented forward one, therefore, Set 2's horses are all one color, and Set 1's horses are all one color.
Finally, Set 1 and Set 2 always overlap, therefore that the color of all Set 1 and Set 2's horses are the same.
...
So, if you hold the 'all horses in a set of size n horses are the same color' assumption as an actually valid assertion, for the sake of argument...
This does logically hold for Set 1 and Set 2 ... but only in isolation, not compared to each other.
The problem is that the sets do not actually always overlap.
If n = 1, and n + 1 = 2, then:
Set 1 = ( 1 )
Set 2 = ( 2 )
No overlap.
Thus the attempted induction falls apart.
Set 1's horse 1 could be brown, Set 2's horse 2 could be ... fucking purple... each set contains only one distinct color, that part is true, but the final assertion that both sets always overlap is false, so when you increment to:
Set 1 = ( 1, 2 )
Set 2 = ( 2, 3 )
We now do not have necessarily have the same colored horse 2 in each set, Set 1's horse 1 and 2 would be brown, Set 2's horse 2 and 3 would be purple.
...
I may be getting this wrong in some way, it's been almost 20 years since I last did set theory / mathematical proof type coursework.
Yep this is the exact issue. This problem comes up frequently in a first discrete math or formal mathematics course in universities, as an example of how subtle mistakes can arise in induction.
I took a peek and it is sort of dumb but logically "sound". Specifically the indictive step.
In the inductive step you assume the statement is true for some number n and use this statement to prove the statement n + 1 is true. If you can do that then you can prove the induction step.
So in this example the statement we assume is true is given n horses, all of them are the same color. To prove the statement for n + 1 horses we look at the n + 1 horses. Then we exclude the last horse. By excluding the last horse we have a set of n horses. By the induction statement this set of horses must all be the same color. So now we've proven the first n horses are the same color.
Next we can exclude the first horse. This also gives us a set of n horses. By the induction statement all these horses must also be the same color. Therefore all n + 1 horses must be the same color.
This sounds really dumb but the proof works in the induction step.
The logical issue is that the base case is wrong which is necessary for a complete proof by induction.
I think? I worked through how the induction logic actually fails.
This kind of induction only works if you can actually prove Sets 1 and 2, starting at n and n+1, actually overlap at all stages... and in this case, they don't.