this post was submitted on 27 May 2024
981 points (100.0% liked)
196
18083 readers
1037 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
Other rules
Behavior rules:
- No bigotry (transphobia, racism, etc…)
- No genocide denial
- No support for authoritarian behaviour (incl. Tankies)
- No namecalling
- Accounts from lemmygrad.ml, threads.net, or hexbear.net are held to higher standards
- Other things seen as cleary bad
Posting rules:
- No AI generated content (DALL-E etc…)
- No advertisements
- No gore / violence
- Mutual aid posts are not allowed
NSFW: NSFW content is permitted but it must be tagged and have content warnings. Anything that doesn't adhere to this will be removed. Content warnings should be added like: [penis], [explicit description of sex]. Non-sexualized breasts of any gender are not considered inappropriate and therefore do not need to be blurred/tagged.
If you have any questions, feel free to contact us on our matrix channel or email.
Other 196's:
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
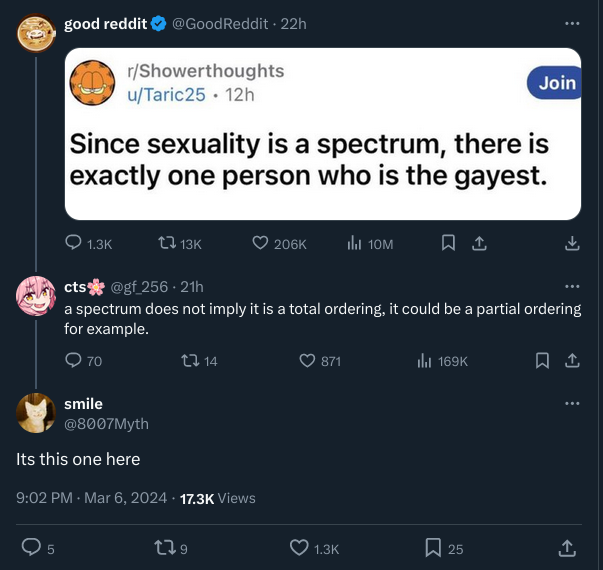
Well that's interesting: in order to define unmeasurable sets, you relied on the axiom of choice... I suppose it might be possible to define unmeasurable sets without AC, but maybe not!
Every time I encounter the axiom of choice implying a bunch of crazy stuff, it always loop back to requiring AC. It's like a bunch of evidence against AC!
I find it interesting that the basic description of AC sounds very plausible, but I'm still convinced mathematicians might have made the wrong choice... (See what i did there? 😄)
It's required, but nontrivially so. It has been proven that ZF + dependent choice is consistent with the assumption that all sets of reals are Lebesgue measurable.